1）某种疾病的患病率是1/1000（即一千个人里有可能有一个人得这个病），用于检查这个疾病的某种检查，对于患者来说有99%的概率检查结果呈阳性，而没有患病的人有99%的概率检查呈阴性。有一天，小明心血来潮去做了这个检查，结果是阳性，你觉得他患病的概率大概是多少呢？凭第一感觉在1秒内回答就好了。

80%～90%？

No，其实只有9%左右。虽然小明的检查结果是阳性，但其实他没有患病的可能性远远高出了患病的可能性，去复查或者做其他精密检查的话，很可能查出来没什么问题。
正确的概率计算应该是：（患病者的比率×阳性概率）/（（患病者的比率×阳性概率）+（非患病者的比率×阳性概率））=0.001×0.99/（0.001×0.99+0.999*0.01）=0.09。这个计算是基于贝叶斯定理（Bayes theorem）。，概率论里应该有学过，看官们可以自行去科普。

这个谬误在日常生活中非常常见，因为人们往往会忽视“患病率只有1/1000”这个事前概率，并且对疾病-阳性结果之间的因果关系过大评价了。下次估计概率时，记得纠正一下自己的算法。

2）某种心理测试，经过很多人的检测证实可靠性比较高。然后你拿来自己测试自己，结果是否可以依照这个心理测试的解释来说明自己的情况呢？

最好别那么做，基本是不准的。

心理测试的“可靠性”是基于收集了大量样本来证实的，难道样本越多不证明它越可靠吗？不是那么回事哦，样本越多，里面每个人的个人差就越被平均化，最后只剩下所有人共通的那个特征，能够被这个心理测试体现出来。拿到一个人身上测，除掉共同特征以外的种种要因，哪怕是做测试时的心情都会成为巨大的影响，要能准确才奇了怪了。有时候我做实验或问卷调查时，被实验参加者问到自己的特征，其实是很难回答的，因为这些测试结果多半不准，写论文的时候我只会用平均值去讨论，绝对不可能拿个例说事，所以被问到时我一般是投其所好，胡诹几句，大家不必当真。

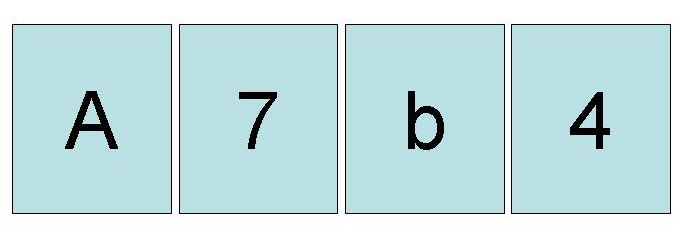
3）以前介绍过的“四张卡片”的实验里，为什么常常会有人选错应该作为证据的卡片呢？因为很多人存在“证实偏误”，对于很多事，只知道考虑确凿的证据，却忽视了反证。比如说“天下乌鸦一般黑”这话，黑乌鸦再多，其实并不能成为证据，如果有一只其他颜色的乌鸦，这话就完全不成立了。法庭上这尤为重要，确凿证据和反证，不是靠数量来抵消的，再怎么有动机有条件的人，只要有一个反证就应该是无罪。遗憾的是，选择性失明的人数不胜数。

截止至2009年11月14日，投票人数达到33人，其中男9名，女22名，未计入性别2名。更新的结果和统计分析结果如下。样本增大后发现，在这点上似乎并没有什么性别差。不过要得出可靠的结论，我觉得至少一两百人的样本吧。

假说为“在go不google剧情上男女有别”时，使用two-tailed test，p = .13，n.s.。

假说为“女人更喜欢google剧情”时，使用one-tailed test, p = .11，n.s.。

---

[OLD]
昨天就 听故事的顺序 码了几句，目前投票人数为28，其中男7名，女19名，未记入性别2名。未计入性别的两票分别为1票go（念“gu”一声），1票不go。记入了性别投票结果为下图，使用“Fisher’s exact test”做了统计分析。

假说为“在go不google剧情上男女有别”时，使用two-tailed test，p = .073，只是有意倾向。

假说为“女人更喜欢google剧情”时，使用one-tailed test, p = .037，significant。

Aoccdrnig to a rscheearch at Cmabrigde Uinervtisy, it deosn’t mttaer in waht oredr the ltteers in a wrod are, the olny iprmoetnt tihng is taht the frist and lsat ltteer be at the rghit pclae.The rset can be a total mses and you can sitll raed it wouthit porbelm. Tihs is bcuseae the huamn mnid deos not raed ervey lteter by istlef, but the wrod as a wlohe.

Amzanig huh?

注：以上为转载。

我没能找到确切的出处。“阅读时，人们是从单词的整体（比如形状、最初和最后的字母），或者视觉上的特征，来想起这个单词的意义”，这个观点很早就已经有不少研究提出来了，但把整段文章的每个词都打乱放到眼前来看，还是觉得很有趣，也给了我一些启示。这里有位研究者对词汇阅读与大脑活动的一些研究文献。

    今天去见了老板，呃，论文得大改特改，Method写得不够清晰，Result的重点不突出，到处是不易看懂的表达……泪奔……如何才能用英文把事情说得清楚易懂呢。。。

    在我的论文的Discussion部分，提出了一个Model来形容空间知识学习的过程，在这里简单介绍下。

    我的论文的主题是研究working memory和spatial knowledge acquisition的关系。首先working memory被假设为一种人在进行思考、计算、理解语言等行为时，用来临时保存信息的一种记忆。它的中心思想是“吃着碗里看着锅里”，饭要下肚，就得先盛到碗里，用于咀嚼（饭=信息，肚子=长期记忆，碗=working memory，咀嚼=处理）。working memory主要有两个部分，一个部分叫做中央处理系(central executive)，用来分配注意的资源;另一个部分是若干个信息储存库，有储存语言信息的phonological loop(PL)、和储存视觉、空间信息的visuospatial sketchpad (VSSP) 。近年的一些研究证明，VSSP应该分割为独立的两部分：视觉信息储存器和空间信息储存器。综上所述，working memory除了有一个中央处理系以外，还有三个信息储存器，分别储存语言、视觉、空间信息。

    Spatial knowledge也被分为3类。第一类是landmark knowledge，指对某一个醒目的标志、或者某个场景的记忆和知识。第二类是route knowledge，指对某一条路线的知识，可以认为是一连串landmark以及连接它们的路径的知识。最后一类叫做survey knowledge，可以认为是一种像地图一样的知识，包括了环境整体的布局、方位、距离等信息。方向感好和不太好的人，主要区别在第三类知识上，方向感不好的人很难获得survey knowledge，没有survey knowledge，也就无法掌握环境整体的样子、不知道如何抄近路。

    在学习三种spatial knowledge时，working memory是起到一个入口加信息过滤的作用。但具体working memory在spatial knowledge acquisition中是如何工作的、三种信息储存器各干啥样的活、方向感好的人和方向感不好的人在使用working memory上有何不同？这些问题目前还不清楚。

    为了讨论这些问题，我做了一些实验室实验。具体方法和结果就不仔细说了，在这里直接介绍一下结论。之前请很多朋友帮忙回答过两次问卷，主要是做为前期做实验计划时的准备、以及验证写discussion时冒出来的一个点子。不过这些问卷的结果最后并没有写入论文，因为问卷涉及到的量表存在一些问题。言归正传，Working memory在spatial knowledge acquisition中起到的作用，可以归纳为下面这张图。

    首先，外界的环境信息进入working memory后，语言信息与空间信息会被抽取出来，用以形成landmark knowledge与route knowledge。而新形成的landmark knowledge和route knowledge需要统合到survey knowledge中，这时就要用到所有的三个存储器（语言、视觉、空间）。在形成landmark knowledge和route knowledge时，视觉信息并没有起到太大作用，或者说没有被作为重点对象抽出来送到长期记忆里面去。主要有两个理由：
    1）只要你睁着眼睛，视觉信息是源源不断地进入working memory的，如果将它们全部都符号化存储到记忆里，认知负荷将会非常大。
    2）人对于landmark以及场景的视觉再认是视角依存的，就是说如果是纯靠视觉信息的话，换个角度再看一个之前记过的场景或landmark，就很难认出来了。所以靠纯视觉信息来认路，是比较靠不住的。

    当然，并不是说人完全不会记住视觉信息，这是违背常理的。视觉信息可能作为一种对物体的记忆而留在长期记忆中。对于空间知识来说，它本身主要作为一种信息输入方式，用于提取语言信息（例如地名、描述），以及检索空间信息。

    方向感不好的人，无法有效地利用空间信息，他们在记忆landmark及场景时，主要靠醒目的标识的描述；记忆一条路时，除了靠描述，还会采用效率不高的视觉信息。换句话说，遇到一个路口需要考虑向哪边拐时，方向感好的人会利用环境的布局、方向来判断，方向感不好的人则会凭“看上去的熟悉感”来判断。语言记忆是很容易淡忘的，所以单靠描述、地名来记路的话遗忘得很快。而视觉记忆则很容易受干扰（类似的东西太多），而且是视角依存，换个角度就认不出来了，所以更容易迷路。

我自己看到的时候是觉得非常不可思议的!一副图片，只有红色和灰色混合而成的像素，但却能产生绿色、蓝色颜色丰富的知觉。眼见为实！
from 東北大栗木先生的主页

原始图片：

1) 在photoshop里抽出红色通道，也就是说下面这幅图片里只有红色。

2) 在photoshop里抽出绿色通道，并且将其黑白化，也就是说下面这幅图片保留了绿色通道的强度，但在颜色上只有灰色像素。

将1和2的图片以合适的比率混合，结果就出来了下面这幅图。照例说红色加灰色，图片应该全都是红红的。但下面这幅图颜色虽然有点暗，但看上去还是很丰富的，而且有明显的蓝色和绿色。事实上每个像素都不可能是蓝色和绿色。如果将局部放大，看看像素的具体颜色。看上去是蓝色或绿色的部分，其实是各种浓度的灰色或者茶色。

这个手法叫做Land’s two color method。这个现象在现实中也可以再现，比如在红色的单色光的照射下，浅灰色的色纸看上去像红色，而深灰色的色纸则看上去像绿色(Helson-Judd effect)。这个现象在脑内机制至今还没有清楚的解释。
E.H. Land, “Color vision and the natural image part II,” Proc. Nat. Acad. Sci., 45, 636-644 (1959).
H. Helson, “Fundamental problems in color vision. I. The principle governing changes in hue, saturation, and lightness of non-selective samples in chromatic illumination,” J. Exp. Psych., 23, 439-477 (1938).

搬新博，总得写点什么。前几天和学部生吃饭的时候，被问到，有没有啥有趣的心理现象。迟疑半天……口头说得清的没几件。在这里简单科普2个，做了实例，形象一点。

1）被欺骗的眼睛
看下面这幅图，图中A和B两块的颜色是不是完全不一样？

再看看下面这幅。

 

 

 

 

 

 

 

 

我可没有改过任何地方的颜色，只是把B移动了一下。为啥B移动的时候颜色看起来好像是越来越深。其实人对亮度的知觉，是根据入射到网膜的光强度（网膜照度）、加上对物体的反射率、入射光的判断综合判断的。反射率×入射光强度=入射到网膜的光强度。A和B入射到网膜的物理刺激是一样的，但是由于对A和B的光源的估计不同（光源A大于B），所以就推断反射率A小于B，也就是说A看上去比较暗。

 

2）四枚卡片
下面有这样4枚卡片放在你面前，每张卡片都是一面是字母，另一面是数字。

 

 

提交以后可以看到答案，你回答对了吗？
这个问题很多人都会选错1枚卡片，原因在问卷的反馈里写了。